Estatística¶
Autor: Felipe Maia Polo - Fundador e ex-presidente do Neuron - Data science and Artificial Intelligence, economista pela USP e mestrando em Estatística pela mesma instituição. Apaixonado por matemática, estatística e data science.
Contato: felipemaiapolo@gmail.com - https://www.linkedin.com/in/felipemaiapolo/
Feedback: https://forms.gle/U6yBVSYwxNRWaE15A
Sugestões de leitura
- Probabilidade: Ross, S. (2014). A first course in probability. Pearson.
- Probabilidade e Estatística: Morettin, P. A., & BUSSAB, W. O. (2017). Estatística básica. Editora Saraiva.
- Análise de Regressão (linear & logística): Wooldridge, J. M. (2015). Introductory econometrics: A modern approach. Nelson Education.
- Machine Learning: James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An introduction to statistical learning (Vol. 112, p. 18). New York: springer.
Nesta parte do conteúdo veremos conceitos de estatística, a sua importância e suas aplicações na análise de dados. Trataremos das principais medidas estatísticas e formulação de gráficos no Python. Serão apresentadas também conceitos ligados à análise de regressão, regressão logística e testes de hipóteses.
O que é estatística?¶
Basicamente, a estatística é um braço da matématica que trabalha com dados para a geração de conhecimento e tomada de decisões. Para isso é necessário entender melhor as características de uma certa população, seja essa de pessoas ou não.
É um tema grandioso que pode ser dividido em duas grandes áreas:
- Análise Exploratória de Dados
- Inferência Estatística
Na análise exploratória de dados, como o nome sugere, o interesse é a familiarização com os dados. Queremos conhecê-los, entender sua estrutura, sua grandeza, especular sobre o que eles querem nos dizer. Já a inferência é um braço da estatística com ênfase na elaboração e testagem de hipóteses sobre características de uma população com base na amostragem, ou seja, com parte da população em nossas mãos, tentamos inferir sobre características da população como um todo.
Em nosso curso (i) vamos falar brevemente da Teoria de Probabilidade, que dá embasamento à análise estatística, (ii) avançar sobre a análise exploratória de dados e ao fim (iii) falaremos um pouco sobre inferência quando estivermos estimando modelos mais complexos.
Conceito de variável aleatória (ou variável)¶
A probabilidade mede o quão provável é a realização de um evento, dadas certas circunstâncias. Para clarear essa ideia: suponha que em uma sala de aula tenhamos 10 alunos, sendo que 3 deles tenham mais de 1,80m. A probabilidade de se tirar aleatoriamente um aluno que tenha mais de 1,80m é $\frac{3}{10}$. Nesse caso, nosso Evento de interesse é tirar um aluno com mais de 1,80m e o Espaço Amostral (conjunto de todas as possibilidades) são os 10 alunos que estão na sala, sendo que apenas 3 têm mais de 1,80m. Se, por exemplo, um desses 3 alunos for substituído por um de 1,70m, o Espaço Amostral muda, alterando também a probabilidade do nosso Evento.
Para continuarmos, é necessário entendermos o que é uma Variável Aleatória - uma variável aleatória é uma forma de representar eventos na forma de números. Voltando ao exemplo da sala de aula, considere a variável aleatória $X$ (geralmente são denotadas por letras maiúsculas) como sendo uma variável binária que assume $1$ caso se tire uma pessoa com altura maior do que 1,80m e $0$ caso contrário, ou seja, estamos represetando um possível evento como o número 1 e outro como o número 0. Então dizemos que a probabilidade de tirarmos uma pessoa maior que 1,80m no caso em que temos 3 pessoas com altura superior a 1,80m entre as 10 pessoas que estão na sala é $P(X=1)=\frac{3}{10}$. Um outro exemplo de variável aleatória seria $Y$, que representa o número de pessoas com mais de 1,80m escolhidas em 2 tentativas. Se consideramos a situação com reposição (ou seja, após escolhermos uma pessoa a retornamos na sala de aula), a probabilidade de se tirar 2 pessoas com mais de 1,80m de altura é igual a $P(Y=2)=\frac{9}{100}$. Na situação sem reposição, teríamos que $P(Y=2)=\frac{3}{10}\frac{2}{9}=\frac{1}{15}$. Em um contexto mais prático, podemos pensar em alguns eventos que podem ser representados por variáveis aleatórias e que são interessantes no campo do Data Science: o salário do brasileiro, gênero das pessoas, idade, nível educacional, uma peça de uma máquina estragar ou não, o número de gols em uma partida de futebol etc.
O que são essas variáveis na prática?¶
O conceito de variável aleatória é um tanto quanto abstrato. Na prática observamos realizações dessas variáveis em nossas bases de dados. Podemos pensar que há uma "lei" oculta que gera os nossos dados, ou seja, que há uma estrutura invisível e mais ou menos estável que nos permite tomar decisões extrapolando conclusões para uma população ou até mesmo fazendo previsões. Observe que se não há estrutura alguma, até mesmo o aprendizado de máquina perde o sentido, pois não haveria padrões explícitos ou implícitos nos dados.
A partir de agora usaremos o termo "variável" de uma maneira mais pragmática que é designar as colunas das nossas bases de dados. A ideia ainda estará ligada àquela de variável aleatória, mas abordaremos a temática de uma forma menos teórica e mais aplicada.
Variáveis e seus tipos¶
Utilizaremos o termo variável para nos referir a alguma característica dos indivíduos que estamos analisando. Para ficar mais claro, vamos utilizar um exemplo. Suponha que tenhamos a seguinte tabela com pessoas e suas características:
| Id | Nome | Idade (Anos) | Peso (Kg) | Grau de Instrução |
|---|---|---|---|---|
| 1 | Felipe | 31 | 80 | Superior |
| 2 | Natália | 43 | 53 | Superior |
| 3 | Augusto | 60 | 74,5 | Médio |
| 4 | Aline | 27 | 63 | Fundamental |
| 5 | Maria | 80 | 63 | Médio |
Antes de qualquer coisa, vamos tentar entender esse conjunto de dados. Temos 5 variáveis, ou seja, 5 características que definem essas pessoas. Portanto, cada característica (variável) é representada por uma coluna da tabela. Vamos começar nossa análise coluna-por-coluna. De imediato percebemos que 3 das 5 variáveis são numéricas e as demais são strings.
Uma divisão muito importante entre tipos de variáveis é entre variáveis quantitativas e qualitativas: as variáveis quantitativas são aquelas que têm grandeza e as qualitativas dizem respeito a qualidades dos sujeitos. Entre as variáveis quantitativas, temos variáveis discretas e variáveis contínuas. A variável Idade é medida em anos inteiros (é uma grandeza) e não admite números quebrados, então é uma variável quantitativa discreta. Já a variável Peso tem grandeza e assume valores contínuos, então é uma variável quantitativa contínua. Entre as variáveis qualitativas, podemos fazer uma divisão entre qualitativas nominais ou qualitativas ordinais. As variáveis Id e Nome são qualitativas nominais, pois não existe nenhuma ordem intrínseca entre as opções e a variável Grau de Instrução é qualitativa ordinal, pois existe uma ordem inerente entre às opções. Muitas vezes as variáveis qualitativas também são conhecidas como variáveis categóricas, por exibirem diversas categorias.
É importante dizer que às vezes é possível encontrar variáveis híbridas, mesclando aspectos quantitativos e qualitativos.
Variáveis com distribuições teóricas de probabilidade¶
O que é uma distribuição de probabilidade? É a forma em que as probabilidades estão distribuídas entre as possíveis opções - se a variável $X$ representa o lançamento do uma moeda honesta, sendo que 0 representa cara e 1 representa coroa, temos que $P(X=0)=\frac{1}{2}$ e $P(X=1)=\frac{1}{2}$, logo essa é a nossa distribuição de probabilidade para a variável $X$. Neste caso, podemos também apresentar a distribuição de $X$ em forma de tabela:
| x | P(X=x) | |
|---|---|---|
| 0 | 1/2 | |
| 1 | 1/2 |
Quando estudamos teoria das probabilidades, aprendemos algumas distribuições teóricas que nos ajudam a modelar o mundo real. Elas são chamadas de "teóricas" porque não existem na natureza de forma perfeita, mas apesar disso são bem úteis para se fazer aproximações e provar resultados matemáticos. Falamos que existem basicamente duas famílias principais de distribuições de probabilidades: as discretas e as contínuas. As discretas são usadas para modelar tanto variáveis qualitativas quanto variáveis quantitativas discretas. Por outro lado, as distribuições contínuas são utilizadas para modelar variáveis quantitativas contínuas. Exemplos de distribuições discretas são:
Distribuição uniforme: todas as alternativas têm a mesma probabilidade. Se há $n$ alternativas $P(X=x)=\frac{1}{n}$ para todo valor $x$ possível. Se uma variável $X$ tem distribuição uniforme discreta, escrevemos assim $X \sim U\{x_1,x_2,...,x_n\}$.
Exercício: se temos um dado não-viciado de 6 lados, então cada um dos lados tem a probabilidade 1/6 de ocorrer em um lançamento. Como eu denotaria a distribuição de X nesse caso?
Vamos programar?
Abrindo as bibliotecas necessárias:
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from pandas import DataFrame
from IPython.display import Image
from IPython.core.display import HTML
Definindo uma função de probabilidade para uma variável com distribuição uniforme:
def unif_disc(x,lista):
if x in lista:
return len(lista)**-1
else:
return 0
Gráfico da distribuição uniforme para o lançamento de um dado:
lista=[1,2,3,4,5,6]
prob=[]
for i in range(10):
prob.append([i,unif_disc(i,lista)])
d=np.array(prob)
d=pd.DataFrame(d)
plot=sns.barplot(x=0,y=1,data=d)
plot.set(ylabel="P(X=x)")
plot.set(xlabel="x")
plt.show()
Distribuição de Bernoulli: a distribuição de Bernoulli é usada para modelar situações em que há duas opções, fracasso e sucesso, sendo que o fracasso é denotado por 0 e o sucesso é denotado por 1. Dizemos que a probabilidade de sucesso é $P(X=1)=p$ e que a probabilidade de fracasso é $P(X=0)=1-p$. Suponha que a probabilidade de se ganhar na loteria em um jogo é $1/1000000=0,0000001$, então podemos definir $p=0,0000001$ como a probabilidade de sucesso. Se a variável $X$ tem distribuição de Bernoulli com parâmetro $p$, escrevemos dessa maneira $X \sim Ber(p)$.
Exercício: dê um exemplo de variável facilmente encontrada em uma base de dados que poderia ser representada por uma variável com distribuição de Bernoulli.
Distribuição binomial: essa distribuição é a soma de $n$ variáveis independentes com distribuição de Bernoulli. Ao invés de eu me perguntar qual a probabilidade de ganhar na loteria em uma tentativa, me pergunto qual a probabilidade de ganhar $k$ vezes em $n$ tentativas indepependentes (ganhar ou perder em uma tentativa não influencia em nada na probabilidade de ganhar ou perder em outra tentativa). Se uma variável $X$ tem distribuição binomial com parâmetros $n$ (número de tantativas) e $p$ (probabilidade de sucesso em uma tentativa), escrevemos $X \sim Bin(n,p)$. Usamos a seguinte fórmula para o cálculo:
\begin{equation} P(X=k)=\binom{n }{k}p^k(1-p)^{n-k}=\frac{n!}{k!(n-k)!}p^k(1-p)^{n-k} \end{equation}Exercício: se a probabilidade de se ganhar na loteria em uma tentativa é $p=0,1$, qual a probabilidade de eu ganhar pelo menos uma vez se eu jogar 20 vezes?
Definindo função de probabilidade para binomial:
import math
def binomial(k,n,p):
factorial=(math.factorial(n)/(math.factorial(k)*math.factorial(n-k)))
return factorial*(p)**k*(1-p)**(n-k)
Gráfico da distribuição binomial:
prob=[]
n=20
p=0.1
from matplotlib.ticker import FuncFormatter
for i in range(n+1):
prob.append([i,binomial(i,n,p)])
d=np.array(prob)
d=pd.DataFrame(d)
plot=sns.barplot(x=0,y=1,data=d)
plot.set(ylabel="P(X=x)")
plot.set(xlabel="x")
plot.xaxis.set_major_formatter(FuncFormatter(lambda x, _: int(x)))
plt.show()
Como foi falado, ainda temos as distribuições contínuas! É importante dizer que quando trabalhamos com distribuições contínuas, temos que $P(X=x)=0$ para todo $x$ e, por isso, deixamos de trabalhar com funções de probabilidade para trabalhar com funções densidades. Vamos então ver alguns exemplos:
Distribuição uniforme contínua: analogamente à distribuição uniforme discreta, a uniforme contínua tem que cada intervalo de mesmo tamanho deve ter a mesma probabilidade de ocorrer. Se $X$ tem distribuição uniforme entre os limites $a$ e $b$, então escrevemos $X \sim U[a,b]$ e sua função densidade é escrita como:
\begin{equation} f(x)=\frac{1}{b-a},\text{ se $x$ está entre $a$ e $b$ (0 caso contrário)} \end{equation}Vamos então ver o gráfico da densidade da uniforme:
#definindo função densidade
def unif_cont(x,a,b):
if x>=a and x<=b:
return 1/(b-a)
else:
return 0
#desenhando gráfico de uma uniforme entre 0 e 1
dens=[]
a=0
b=1
x = np.arange(-.5, 1.5, 0.001)
for i in x:
dens.append(unif_cont(i,a,b))
d=np.array(dens)
plot=plt.plot(x,d)
plt.ylabel("f(x)")
plt.xlabel("x")
plt.show()
Exercício: neste cenário, se $X$ tem distribuição uniforme entre 0 e 1, qual a probabilidade de tirarmos um valor entre 0,5 e 0,75? Basta calcular a área entre o gráfico da função densidade e o eixo $x$ entre os valores 0,5 e 0,75. Logo, temos que essa probabilidade é 0,25.
Distribuição Normal: Uma distribuição contínua muito importante e muito conhecida é a distribuição Normal. Ela é uma das mais incríveis e úteis distribuições teóricas que existem e é capaz de aproximar diversos fenômenos da natureza. Ela é conhecida por ser simétrica e ter densidade no formato de um sino. A função densidade da normal também pode ser chamada por curva gaussiana, em homenagem ao metemático Gauss. Se uma variável $X$ tem distribuição normal com média $\mu$ e variância $\sigma ^2$ (que é uma medida de quão dispersos serão seus valores aleatórios), podemos escrever $X \sim N(\mu,\sigma ^2)$. Se $Z \sim N(0,1)$, dizemos que $Z$ é distribuída conforme uma Normal Padrão. A função densidade da normal tem a fórmula:
\begin{equation} f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{1}{2}\big(\frac{x-\mu}{\sigma}\big)^2} \end{equation}Ex. o Q.I. (quoeficiente de inteligência) for modelado pelos psicólogos para ter distribuição $N(100,15^2)$. Vamos simular a distribuição do Q.I. na população:
#definindo função densidade
def normal(x,mu,sigma):
frac=1/np.sqrt(2*np.pi*sigma**2)
return frac*np.e**(-.5*((x-mu)/sigma)**2)
#desenhando gráfico de uma normal
dens=[]
mu=100
sigma=15
x = np.arange(40, 160, 0.001)
for i in x:
dens.append(normal(i,mu,sigma))
d=np.array(dens)
plot=plt.plot(x,d)
plt.ylabel("f(x)")
plt.xlabel("x")
plt.show()
Exercício: de acordo com o gráfico acima, o que é mais provável, uma pessoa qualquer ter QI entre 100 e 120 ou entre 140 e 160?
Um atributo muito legal e importante que o Python tem em suas dependências é a capacidade da geração de números "aleatórios" de acordo com uma distribuição específica. Por exemplo, se quisermos gerar números de acordo com uma distribuição uniforme contínua entre 0 e 1 podemos usar o pacote Numpy de acordo com o mostrado a seguir:
#o primeiro parâmetro é o limite inferior da distribuição, o segundo é o limite superior e o terceiro é o tamanho da amostra
a=0
b=1
N=25
np.random.seed(42) #fixando semente
x=np.random.uniform(a,b,N)
#Visualizando vetor gerado
print(x)
Podemos visualizar a distribuição desses números gerados aleatóriamente utilizando um gráfico de densidade (+ comum, por se tratar de uma variável com distribuição contínua), um histograma ou os dois juntos:
sns.distplot(x,hist=False)
plt.show()
sns.distplot(x,kde=False)
plt.show()
sns.distplot(x)
plt.show()
Apesar de termos gerado uma amostra com distribuição uniforme, o gráfico não parece tão "uniforme" assim, né? Isso porque nossa amostra é muito pequena. Se gerarmos uma amostra com N=1.000.000, por exemplo, o cenário já muda drasticamente:
a=0
b=1
N=1000000
np.random.seed(42) #fixando semente
x=np.random.uniform(a,b,N)
sns.distplot(x,hist=False)
plt.show()
sns.distplot(x,kde=False)
plt.show()
sns.distplot(x)
plt.show()
Se quisermos simular, por exemplo, o lançamento de uma moeda (distribuição Bernoulli), podemos simular uma variável uniforme entre 0 e 1 e se o valor tirado for menor do que 0.5 dizemos que foi cara e se for maior dizemos que foi coroa (ou vice-versa). Mantemos a probabilidade de 50% em cada caso.
Vamos então simular o lançamento de uma moeda:
x=np.random.uniform(0,1,1)
print("x=",x, "\n")
if x<0.5: print("Cara!")
else: print("Coroa!")
Aplicação: estimando o tempo de um projeto com simulação de Monte Carlo¶
Simulação de Monte Carlo é basicamente simular processos de acordo com distribuições de probabilidade e com isso ser capaz de fazer estimações muito bem feitas. Vamos à prática que ficará mais fácil e mais interessante de se entender!
Suponha que queremos descrever a distribuição de probabilidade de dias que um projeto demorará para ficar pronto. Suponha inicialmente que esse projeto seja composto de uma primeira tarefa que é criar um algoritmo capaz de limpar uma base de dados. Suponha que essa é uma tarefa que levará de 2 a 4 dias, sendo que a probabilidade de a tarefa ficar pronta ao final do 2º dia é 0.2, de ficar pronta ao final do 3º dia é 0.35 e de ficar pronta ao final do 4º dias é 0.45.
Se $D_1$ é uma quantidade aleatória de dias para se completar a primeira tarefa, temos então que:
- $P(D_1=1)=0$
- $P(D_1=2)=0.2$
- $P(D_1=3)=0.35$
- $P(D_1=4)=0.45$
Vamos então simular a variável $D_1$ assim como fizemos com o lançamento da moeda. Podemos aplicar o resultado diretamente com o pacote Numpy, não sendo necessário gerar a uniforme e depois usar condicionais em sequência, podemos usar um gerador de variáveis aleatórias multinomiais (uma generalização de Bernoulli, pois podem haver mais de 2 opções de resultado):
d=[2,3,4] #lista de dias possíveis
prob=[.2,.35,.45] #probabilidades por dias
N=10 #número de lançamentos
np.random.seed(42) #fixando semente
x=np.random.multinomial(N, prob)
x
O resultado acima quer dizer que em 10 repetições, uma das vezes demorou-se 1 vez para terminar a tarefa ao final do segundo dia, por exemplo. Vamos agora repetir o experimento com N=100.000:
d=[2,3,4] #lista de dias possíveis
prob=[.2,.35,.45] #probabilidades por dias
N=100000 #número de lançamentos
np.random.seed(42) #fixando semente
x=np.random.multinomial(N, prob)
x
Podemos acessar as probabilidades empíricas (proporções) de cada uma das possibilidades dividindo x por N:
x/N
Perceba que as probabilidades empíricas são muito próximas àqueles que definimos inicialmente. Esse exemplo não traz nada de muito interessante pois sabemos as probabilidades de antemão de se terminar o projeto de uma tarefa. No entanto, quando começamos a adicionar tarefas em série ou em paralelo, as coisas se tornam complicadas e muitas vezes calcular na "raça" a distribuição de dias para terminar o projeto é inviável.
Vamos fazer um exemplo para duas tarefas em série. Vamos supor que a primeira tarefa continue sendo a mesma (limpeza da base de dados) com as mesmas probabilidades associadas. Agora temos uma segunda tarefa, que será executada logo após o término da primeira, mas que a quantidade de dias para o término é independente dos dias gastos para a primeira tarefa (uma hipótese simplificadora e realista). Suponha que a segunda tarefa seja gerar resultados estatísticos a partir dos dados tratados e que os dias para seu término, $D_2$, tenham a seguinte distribuição de probabilidade:
- $P(D_2=1)=.3$
- $P(D_2=2)=.4$
- $P(D_2=3)=.3$
Agora que sabemos a distribuição de $D_1$ e $D_2$, queremos saber a distribuição de dias para o términar do projeto como um todo $D=D_1+D_2$. Vamos então aproximá-la fazendo simulações! Como, a princípio, as tarefas podem ocorrer tanto em série quanto em paralelo, vamos simular dentro de um loop, sendo que cada iteração corresponde a uma execução do projeto como um todo. Em uma iteração qualquer, sortearemos um número aleatório de dias para a conclusão da primeira tarefa, sortearemos um número aleatório de dias para a conclusão da segunda tarefa e depois somaremos os dois números, obtendo o número total daquela iteração:
d1=[2,3,4] #lista de dias possíveis
p1=[.2,.35,.45] #probabilidades por dias
d2=[1,2,3] #lista de dias possíveis
p2=[.3,.4,.3] #probabilidades por dias
d=[]
N=100000 #número de lançamentos
np.random.seed(42) #fixando semente
for i in range(N):
x1=list(np.random.multinomial(1, p1))
x2=list(np.random.multinomial(1, p2))
d.append(d1[x1.index(1)] + d2[x2.index(1)])
Os dias para a conclusão do projeto completo foram armazenados na lista "d". Vamos verificar a distribuição de dias! Vamos transformar nossa lista em um dataset do Pandas para conseguir trabalhar com algumas ferramentas deste pacote:
d={'dias':d}
d=pd.DataFrame(d)
Vamos utilizar uma tabela de frequências para a análise:
pd.crosstab(index=d['dias'], columns="freq")
Agora visualizando as frequências relativas:
d_plot=pd.crosstab(index=d['dias'], columns="freq_rel", normalize=True)
d_plot
Agora vamos visualizar graficamente a distribuições de dias para a conclusão do projeto:
d_plot['dias']=d_plot.index
plot=sns.barplot(x='dias',y='freq_rel',data=d_plot)
plot.set(ylabel="Probabilidade empírica")
plot.set(xlabel="Término do projeto (Dias)")
plt.show()
print("O número médio de dias pra o término do projeto é de:", d['dias'].mean(),"dias.")
Exercício: como estão organizadas as tarefas de um projeto que tem uma variável aleatória de dias até o término do projeto com a seguinte cara $D=D_0+max(D_1,D_2+D_3)+D_4$?
Sugestão:¶
Episódio Hang the DJ da série Black Mirror.
Como entender as informações que as variáveis querem nos passar?¶
Com o intuito de extrair informações relevantes para nossas análises, vamos utilizar medidas para descrever nossos dados além de alguns métodos gráficos. As medidas que usaremos dependem essencialmente dos tipos de variáveis que estamos trabalhando.
Descrevendo a base de dados que utilizaremos¶
A partir de agora, vamos trabalhar com uma base de dados real retirada da plataforma Kaggle. A base se chama House Sales in King County, USA e se trata de uma base de dados contendo características de mais de 20 mil imóveis de uma região do estado de Washington nos EUA. Os links para acessar a base são https://www.kaggle.com/harlfoxem/housesalesprediction e https://rstudio-pubs-static.s3.amazonaws.com/155304_cc51f448116744069664b35e7762999f.html.
Aqui vai uma breve descrição da base:
Essa base de dados contém preços de casas vendidas em King County, nos EUA. A base é uma amostra das vendas no local entre Maio 2014 e Maio 2015
id: ID para a casa
date: Data em que a casa foi vendida
price: Preço em que a casa foi vendida
bedrooms: Número de quartos na casa
bathrooms: Número de banheiros na casa (banheiros mais ou menos completos têm pesos diferentes)
sqft_living: Área dentro do imóvel (em pés quadrados)
sqft_lot: Área do lote (em pés quadrados)
floors: Número de andares
waterfront: Variável indicadora se o imóvel tem vista para o mar
view: Um índice de 0 a 4 de quão boa era a vista da propriedade
condition: Um índice de 1 a 5 na condição do imóvel
grade: Um índice de 1 a 13, no qual 1-3 o imóvel tem um baixo nível de construção e design, 7 tem um nível médio de construção e design, e 11-13 têm um alto nível de qualidade de construção e design.
sqft_above: A área do espaço habitacional interior que está acima do nível do solo
sqft_basement: Área do porão
yr_built: Data de construção
yr_renovated: Data da última reforma
zipcode: CEP
lat: Latitude
long: Longitude
sqft_living15: Área média dentro dos imóveis (em pés quadrados) dos 15 vizinhos mais próximos
sqft_lot15: Área média dos lotes (em pés quadrados) dos 15 vizinhos mais próximos
Exercício:
Classifique cada uma das variáveis.
Abrindo a base de dados com pandas:
data=pd.read_csv("kc_house_data.csv")
Vamos utilizar a função .head() para ter uma primeira impressão da base de dados que temos em mãos:
data.head()
Vamos também explorar o tipo de cada uma das variáveis:
data.dtypes
Vamos também contar quantas observações temos por variável:
data.count()
Antes de começar a explorar mais a fundo a base, vamos tornar as variáveis mais interpretáveis (forma de feature engineering). Primeiramente vamos categorizar as notas para a arquitetura do apartamento entre baixa (1-5), média (5-10) e alta (11-13), como sugerido pela descrição da base de dados (demos uma mudadinha aqui, mas tudo bem):
data['design']=np.where(data['grade']<=5, 'Baixa',
np.where((data['grade']>5) & (data['grade']<=10), 'Média',
np.where(data['grade']>10, 'Alta','')))
data['design']=pd.Categorical(data['design'], categories=["Baixa", "Média", "Alta"], ordered=True)
Vamos criar uma variável que denota o ano em que a casa foi vendida com base na data:
data['ano']=data['date'].str[:4]
data['ano']=data['ano'].astype('int64')
Agora vamos criar uma variável categórica de idade do imóvel com as categorias velho (idade>=30), intermediário (10<=idade<30) e novo (idade<10):
data['idade_ano']=data['ano']-data['yr_built']
data['idade']=np.where(data['idade_ano']>=30, 'Velho',
np.where((data['idade_ano']>=10) & (data['idade_ano']<30), 'Intermediário',
np.where(data['idade_ano']<10, 'Novo','')))
data['idade']=pd.Categorical(data['idade'], categories=["Velho", "Intermediário", "Novo"], ordered=True)
Conforme formos explorando os nossos dados, vamos fazendo mais coisas.
Variáveis qualitativas¶
Quando trabalhamos com esse tipo de variável, geralmente reportamos em forma de tabelas medidas de frequência (contagem por categoria) ou de frequência relativa (% por categoria), além também de utilizarmos os famosos histogramas para tornar essas informações visuais. Perceba que temos algumas variáveis qualitativas como, por exemplo, se a casa dá ou não vista para o mar ou o nível da arquitetura da casa. Vamos descrever essa última:
Vamos então colocar a mão na massa!
Primeiramente vamos construir uma tabela de frequência para a variável de arquitetura:
pd.crosstab(index=data['design'], columns="Fequência")
Podemos também trabalhar com propoções:
pd.crosstab(index=data['design'], columns="Fequência Relativa", normalize=True)
Quando trabalhamos com proporções (frequências relativas), na realidade estamos trabalhando com aproximações para as probabilidades da realizações de eventos aleatórios. Dizemos então que estamos aproximando a distribuição de probabilidades da variável em questão - é comum dizer que estamos trabalhando com a distribuição empírica da variável.
Exercício: como interpretar de um ponto de vista teórico (falando em eventos, variáveis aleatórias e distribuições) o resultado abaixo?
pd.crosstab(index=data['idade'], columns="Fequência Relativa", normalize=True)
Além de visualizar as distribuições empíricas das nossas variáveis em forma de tabela, também é importante colocar os resultados em forma gráfica:
plot = sns.countplot(x='idade', data=data)
plot.set(ylabel="Quantidade")
plot.set(ylabel="Idade do imóvel")
plt.show()
Podemos também observar os resultados para as frequências relativas:
d=pd.crosstab(index=data['idade'], columns="freq_rel", normalize=True)
d["idade"]=d.index
plot=sns.barplot(x='idade',y='freq_rel',data=d)
plot.set(ylabel="Frequência Relativa")
plot.set(xlabel="Idade do imóvel")
plt.show()
Variáveis quantitativas¶
Quando trabalhamos com esse tipo de variável, geralmente as descrevemos com a ajuda de medidas resumo ou estatísticas, além de utilizarmos gráficos como histogramas, densidades e box-plots. Perceba que temos algumas variáveis quantitativas em nossa base de dados como, por exemplo, idade do imóvel em anos, preço do imóvel, número de quartos, área do imóvel etc. Perceba que algumas das variáveis citadas são contínuas enquanto outras são discretas.
Vamos então colocar a mão na massa!
Primeiramente vamos falar um pouco sobre as medidas resumo/estatísticas de uma forma mais teórica:
Média¶
Vamos começar pela mais famosa das medidas de posição: a média. Esta é uma estatística, uma medida, que resume os dados em um apenas um único valor, e é definida como a soma das observações de uma sequência de valores dividida pela quantidade de elementos dessa sequência. Confira a expressão:
\begin{equation} \bar{x} = \frac{1}{n}\sum_{i=1}^{n} x_i \end{equation}Pra ficar mais claro, vamos calcular a média de uma variável X (pode ser a idade de um grupo de pessoas, por exemplo):
x=[31,43,60,27,31]
n=len(x)
media_x=(n**-1)*(x[0]+x[1]+x[2]+x[3]+x[4])
print ("A média de x é: ",media_x)
Quando calculamos a média com dados da população inteira, dizemos que temas a média populacional e trocamos $\bar{x}$ por $\mu$ e $n$ por $N$. Por outro lado, quando temos uma amostra (de preferência aleatória) da população, que é o que acontece na maioria das vezes, dizemos que estamos calculando a média amostral. Além da média amostral ser informativa por si só, ela oferece um ótimo estimador para a média populacional, ou seja, uma fórmula que permite a estimação de uma característica (parâmetro) populacional.
Mediana¶
A segunda medida que vamos utilizar é a mediana. Trata-se da observação central de uma sequência de dados ordenada. Perceba que a mediana somente será exatamente o termo central de uma série de dados quando essa sequência tiver um número ímpar de elementos. Quando a série de dados tiver um número par, a mediana será definida como a média entre os dois termos centrais. Ou seja:
\begin{array}{cc} x_{(\frac{n+1}{2})}, \text{se n é ímpar} \\ \frac{x_{(\frac{n}{2})}+x_{(\frac{n}{2}+1)}}{2}, \text{se n é par} \end{array}Pra ficar mais claro, vamos calcular a mediana de uma variável X, com um número ímpar de observações, e uma variável Y, com um número par de observações:
#Entrando com os dados de Idade e Peso:
x=[31,43,60,27,31]
y=[9,3,4,7,6,-8]
#Criando função para o cálculo da mediana
def mediana(z):
n=len(z)
z.sort()
if n%2 == 1:
index=int(((n+1)/2)-1)
return z[index]
else:
index=int((n/2)-1)
return (z[index]+z[index+1])/2
print("As medianas das variáveis X e Y são, respectivamente ", mediana(x)," e ", mediana(y))
Dado o método de cálculo da mediana, que leva em conta apenas os termos centrais, temos que essa medida, diferentemente da média, é robusta com relação à valores extremos. Em outras palavras, outliers têm grande inflcuencia no valor da média, mas não no valor da mediana. Vejamos X e Y ordenadas:
X: 27, 31, 31, 43, 60
Y: -8, 3, 4, 6, 7, 9
Moda¶
Outra medida resumo (de posição) que temos é a Moda. Como o próprio nome já diz, ela busca o(s) elemento(s) que está(ão) na moda, ou seja, os elementos que mais se repetem, que aparecem com maior frequencia numa sequência de dados. A moda da variável X é 31, por exemplo. Quando temos uma variável contínua, podemos pensar na moda como sendo o valor com maior densidade.
Percentis, Decis, Quintis e Quartis¶
Todas essas medidas de posição são análogas à mediana. A mediana é o valor da posição central da distribuição, ou seja, 50% dos valores são menores ou iguais à mediana e 50% dos valores são maiores e iguais à mediana. Quando falamos em percentis, ao invés de dividirmos a distribuição em 2 partes (como na mediana), dividimos a distribuição em 100 partes e pegamos a valor da parte que nos interessa - perceba que o 50º percentil á igual à mediana. Os decis, quintis e quartis seguem a mesma ideia, mas dividindo a distribuição em 10, 5 e 4 partes com a mesma quantidade de valores. Lembre que sempre devemos ordenar os valores antes de calcularmos essas medidas de posição.
Variância¶
A variância, ao contrário do vimos até o momento, é uma medida para o grau de variação (dispersão) dos dados. Ao contrário da média, as variâncias populacionais e amostrais têm fórmulas distintas (se quiser mais detalhes, pesquisar sobre estimadores viesados e não viesados) e que convergem quando o tamanho da amostra é grande o bastante. Isso quer dizer que quando estamos trabalhamos com uma população inteira, devemos utilizar a seguinte fórmula:
\begin{equation} Var(X) = \sigma ^2 =\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2 \end{equation}Se estamos trabalhando com uma amostra aleatória da população e queremos estimar a variância populacional, utilizamos a seguinte fórmula:
\begin{equation} Var(x) = S^2 =\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2 \end{equation}Calculando a variância da variável X para os casos amostral e populacional:
x=[31,43,60,27,31]
n=len(x)
media_x=(n**-1)*(x[0]+x[1]+x[2]+x[3]+x[4])
var_x_a=((n-1)**-1)*((x[0]-media_x)**2+(x[1]-media_x)**2+(x[2]-media_x)**2+(x[3]-media_x)**2+(x[4]-media_x)**2)
var_x_p=((n)**-1)*((x[0]-media_x)**2+(x[1]-media_x)**2+(x[2]-media_x)**2+(x[3]-media_x)**2+(x[4]-media_x)**2)
print("A variância para o caso amostral é ",var_x_a)
print("A variância para o caso populacional é ",var_x_p)
Exercício: existe variância negativa? Por quê?
Desvio-Padrão¶
Apesar de a variância ser uma boa medida de dispersão dos dados, o seu resultado apresenta sempre o quadrado de sua dimensão, isto é, de sua unidade de medida. Por exemplo, se a variância for calculada sobre uma sequência de dados de peso de pessoas, o resultado será acompanhado da unidade $Kg^2$ e isso pode gerar um pouco de dificuldade de interpretação dos resultados e de possíveis comparações.
Para contornar essa situação, podemos utilizar outra medida de dispersão, o desvio-padrão, que é exatamente a raiz quadrada da variância. Dessa forma, o problema da dimensão fica resolvido. Assim como a variância, temos o desvio-padrão para o caso populacional e para o caso amostral. Segue a expressão do desvio-padrão para o caso amostral:
\begin{eqnarray} dp(x) =\sqrt{Var(x)}=S \end{eqnarray}E para o caso populacional, temos:
\begin{eqnarray} dp(X) =\sqrt{Var(X)}=\sigma \end{eqnarray}Vamos calcular os desvios-padrão para os valores X:
dp_x_a=np.sqrt(var_x_a)
dp_x_p=np.sqrt(var_x_p)
print("O desvio-padrão para o caso amostral é ",dp_x_a)
print("O desvio-padrão para o caso populacional é ",dp_x_p)
Coeficiente de Variação¶
Além de todas essas medidas, temos outra que combina duas das que já vimos aqui e que nos permite fazer comparações entre sequências distintas, pois está livre de qualquer unidade/dimensão. Trata-se de uma medida absoluta, o coeficiente de variação, que é definido da seguinte maneira:
\begin{equation} CV(x) = \frac{dp(x)}{\bar{x}} \end{equation}Para o caso amostral, vamos calcular o CV de x:
print("O coeficiente de variação da variavel X é igual a ",dp_x_a/media_x)
Análise descritiva para dados quantitativos¶
Agora que sabemos as principais medidas para se análisar dados quantitativos, vamos nos concentrar em analisar algumas das variáveis em nossa base de dados de imóveis. Vamos analisar uma variável quantitativa discreta e uma contínua. Primeiramente, vamos nos concentrar em uma variável discreta, que pode ser o número de quartos em cada uma das casas:
data['bedrooms'].describe()
A função describe é uma função para bases de dados (data frames) do Pandas. Ela é muito boa, porque nos dá as principais medidas descritivas de uma forma direta. Lembre que o desvio-padrão tem tanto uma versão para populações quanto uma versão para amostras - quando ficamos na dúvida qual o valor reportado pela função do pacote é necessário checar a documentação do mesmo. Nesse caso, temos que std é o dp amostral, min é o valor mínimo da amostra (percentil 0), 25% é o primeiro quartil, 50% é a mediana (ou segundo quartil), 75% é o terceiro quartil e max é o valor máximo na amostra (centésimo percentil).
A forma gráfica mais direta para a visualização desses dados seria utilizando um histograma:
d=pd.crosstab(index=data['bedrooms'], columns="freq_rel", normalize=True)
d['bedrooms']=d.index
plot=sns.barplot(x='bedrooms',y='freq_rel',data=d)
plt.ylabel('Frequência relativa')
plt.xlabel('Número de quartos')
plt.show()
É possível perceber que há alguns outliers em nossa amostra. Para melhorar a visualização para a maioria dos nossos pontos na amostra, vamos restringir a amostra para alguns valores:
d=pd.crosstab(index=data['bedrooms'], columns="freq_rel", normalize=True)
d['bedrooms']=d.index
plot=sns.barplot(x='bedrooms',y='freq_rel',data=d)
plt.ylabel('Frequência relativa')
plt.xlabel('Número de quartos')
plt.xlim(left=.5,right=7.5)
plt.show()
Uma outra forma interessante de visualizar a distribuição de uma variável quantitativa é ordenando sua amostra e plotando os dados:
x=data['bedrooms']
x=np.array(x)
x=np.sort(x)
plt.ylabel('Número de quartos')
plt.xlabel('Posição do imóvel')
plt.plot(x, 'bo')
plt.show()
É possível checar a discreticidade da variável pelas parte constante ("deitadas") do gráfico. Agora que já vimos um exemplo de análise descritiva para variáveis quantitativas discretas, veremos algumas análises para uma variável quantitativa contínua: o preço do imóvel. Primeiramente, tiraremos as principais estatísticas, como já fizemos:
data['price'].describe()
Agora vamos ver os principais gráficos de distribuição. Vamos começar com um gráfico de densidade:
plot=sns.distplot(data['price'],hist=False)
plt.ylabel('Densidade')
plt.xlabel('Preço')
plt.xticks(rotation=30)
plt.show()
Assim como já vimos no caso do número de quartos, temos outliers presentes. Vamos "cortar" a distribuição para termos uma melhor noção do que os dados querem nos passar. Além disso, vamos plotar uma versão discretizada dessa variável com um histograma ao fundo:
plot=sns.distplot(data['price'],hist=True)
plt.ylabel('Densidade')
plt.xlabel('Preço')
plt.xlim(left=0,right=2000000)
plt.xticks(rotation=30)
plt.show()
Exercício: olhando para o gráfico de densidade acima, onde está a moda desta distribuição? A média está à esquerda ou à direita da moda? A mediana está à esquerda ou à direita da média?
Assim como fizemos no exemplo anterior. Vamos ordenar as casas por seus preços e plotar os valores:
x=data['price']
x=np.array(x)
x=np.sort(x)
plt.ylabel('Preço do imóvel')
plt.xlabel('Posição')
plt.plot(x, 'bo')
plt.show()
Exercício: qualitativamente, qual a diferença do gráfico acima e do passado?
O gráfico acima pode ser muito útil quando queremos mostrar qual a posição de uma certa observação em relação às outras. Nesse caso queremos deixar em destaque um certo imóvel, o de número 13000 (posição de seu preço):
x=data['price']
x=np.array(x)
x=np.sort(x)
plt.plot(x)
y=np.full(np.shape(x), np.nan)
y[13000]=x[13000]
plt.ylabel('Preço do imóvel')
plt.xlabel('Posição')
plt.plot(y, 'ro', markersize=10)
plt.show()
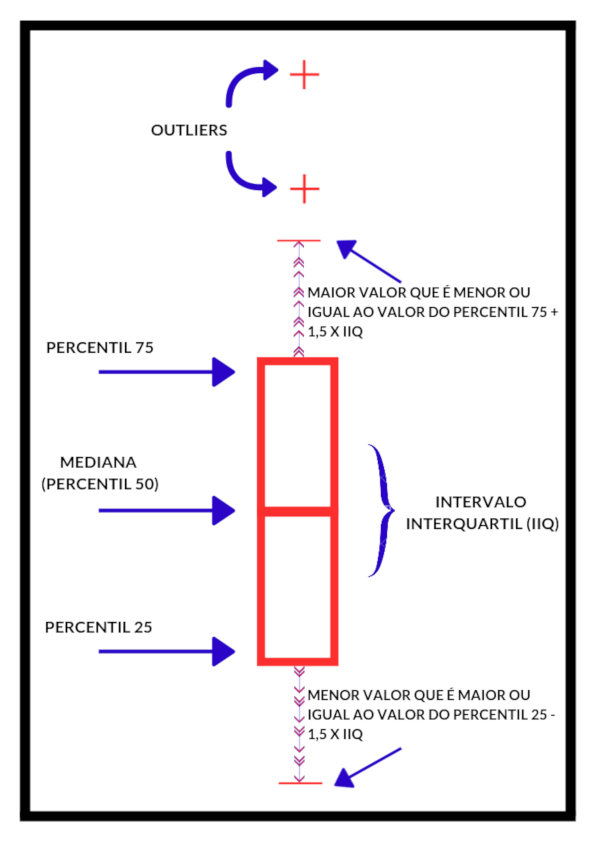
Um outro tipo de gráfico que ainda não foi apresentado e que é muito utilizado pelos estatísticos é o box-plot. A interpretação será feita da seguinte forma:
Image(url= "p1.png", width=400, height=300)
Adaptado de: http://www.bom.gov.au/water/ssf/faq/boxplot.png
No box-plot é possível ver graficamente algumas das principais medidas de posição já apresentadas:
sns.boxplot(data['price'])
plt.xlabel('Preço do imóvel')
plt.xticks(rotation=30)
plt.show()
sns.boxplot(data['price'])
plt.xlim(left=0,right=1300000)
plt.xlabel('Preço do imóvel')
plt.show()
Distribuição conjunta de duas variáveis¶
Até o momento nos concentramos em entender como as variáveis estão distribuídas isoladamente. Nesta seção vamos trabalhar com distriuições conjuntas de duas variáveis (na teoria, poderíamos trabalhar com múltiplas variáveis, mas não seria didático). Isso quer dizer que vamos enxergar duas variáveis como um vetor de variáveis. Antes de começarmos a trabalhar com os dados que temos, vamos fazer uma pequena introdução teórica do que significa ver duas variáveis como um vetor de variáveis.
Imagine que lançamos duas moedas honestas e temos que a variável $X_j=1$ se tiramos cara para a j-ésima moeda e $X_j=0$ se tirarmos coroa para a j-ésima moeda. Dessa maneira temos que $P(X_j=1)=P(X_j=0)=1/2$ para $j=1,2$. Quando avaliamos a distribuição conjunta de $X_1$ e $X_2$, na verdade estamos avaliando a distribuição do vetor $X=(X_1,X_2)$. A distribuição de $X$ pode ser verificada calculando-se probabilidades deste tipo $P(X_1=x_1,X_2=x_2)$, sendo que neste caso $x_1$ e $x_2$ podemos ser iguais a 0 ou 1. Dizemos que estamos trabalhando com a distribuição conjunta de duas variáveis porque queremos saber a probabilidade de que $X_1$ seja igual a $x_1$ e que $X_2$ seja igual a $x_2$ simultaneamente. Um exemplo concreto seria o cálculo da probabilidade de tirarmos cara na primeiro primeiro lançamento e coroa no segundo que é $P(X_1=1,X_2=0)=1/4$. A distribuição de probabilidades de $X$ pode ser vista na tabela abaixo:
| $X_1$, $X_2$ | 0 | 1 |
|---|---|---|
| 0 | 1/4 | 1/4 |
| 1 | 1/4 | 1/4 |
No exemplo acima, o vetor aleatório $X$ é qualitativo e discreto em suas duas entradas $X_1$ e $X_2$, mas não precisaria ser assim. Podemos misturar todos os tipos de variáveis para formar um vetor aleatório. Um caso importante é quando temos duas variáveis quantitativas contínuas - nesse caso, assim como no caso univariado, falamos em funções densidades e não de funções de probabilidade. Se $X$ e $Y$ são variáveis quantitativas contínuas, trabalharemos com a densidade conjunta das variáveis $f(x,y)$ se quisermos avaliar suas distribuição conjunta. Mais a frente veremos exemplos práticos de como esses conceitos aparecem na realidade.
Vamos primeiramente avaliar as distribuições conjuntas de variáveis qualitativas e quantitativas discretas. Veremos a seguir a distribuição empírica da variável design e da variável idade dos imóveis:
tab=pd.crosstab(data['design'],data['idade'], normalize=True)
tab
O Pandas também oferece a opção de visualizarmos esta tabela de uma diferente maneira:
pd.crosstab(index=[data['design'],data['idade']],columns="Frequência relativa", normalize=True)
Considerando a primeira maneira, podemos fazer uma visualização da nossa tabela de maneira visual utilizando um heatmap:
sns.heatmap(tab, cmap="Greys")
plt.ylabel('Nota em design')
plt.xlabel('Idade do imóvel')
plt.show()
Com a ajuda do heatmap, podemos ver claramente que a distribuição de concentra na linha do meio, em que o design tem uma nota média. Isso realmente faz sentido, pois a grande maioria dos imóveis têm uma nota média (96,4%). Vamos avaliar a distribuição conjunta de mais duas variáveis discretas, o número de andares e o número de quartos:
tab=pd.crosstab(data['floors'],data['bedrooms'], normalize=True)
tab
Neste caso, como temos uma grande quantidade de linhas e de colunas, fica muito difícil de tiramos informações relevantes somente olhando para a tabela. Vamos então traduzir esta tabela para a forma gráfica do heatmap:
sns.heatmap(tab, cmap="Greys")
plt.ylabel('Número de andares')
plt.xlabel('Número de quartos')
plt.show()
Antes de começarmos a verificar a distribuição conjunta de variáveis contínuas, vamos falar de algumas medidas resumo para distribuições conjuntas, assim como fizemos para as distribuições univariadas.
Coeficiente de correlação de Pearson¶
O coeficiente de correlação de Pearson é uma medida de relação linear entre duas variáveis que varia de -1 a 1, sendo que -1 nos diz que as variáveis tem uma relação linear perfeita e negativa, 0 nos diz que as variáveis não tem relação linear e 1 nos diz que as variáveis tem relação linear perfeita positiva. As versões populacionais e amostrais desta medida coincidem e são dadas pela fórmula:
\begin{equation} corr(x,y) = \rho_{xy} =r=\frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2\sum_{i=1}^{n}(y_i - \bar{y})^2}} \end{equation}Na imagem abaixo temos alguns cálculos de $\rho_{xy}$ para alguns exemplos de scatter plots:
def plot_cor(r):
print("Correlação de Pearson =",r)
mean = [0, 0]
cov = [[1, r], [r, 1]]
x, y = np.random.multivariate_normal(mean, cov, 800).T
plt.plot(x, y, 'bo')
plt.axis('equal')
plt.show()
r=1 #Correlação
plot_cor(r)
r=.5 #Correlação
plot_cor(r)
r=0 #Correlação
plot_cor(r)
r=-.8 #Correlação
plot_cor(r)
Tau de Kendall¶
Uma outra medida muito útil e que é pouco ensinada é o Tau de Kendall. Esta medida também varia de -1 a 1, sendo que ela capta relações de concordância entre duas variáveis sem que essa relação tenha que linear. Funciona como uma "correlação de rankings". Vamos usar essa medida e se você quiser ler mais a respeito, sugiro o Wikipedia https://en.wikipedia.org/wiki/Kendall_rank_correlation_coefficient.
Visualizando distribuições conjuntas contínuas¶
Agora que já sabemos como interpretar o coeficiente de correlação de Pearson, vamos ver graficamente como duas variáveis quantitativas se distribuem conjuntamente. Antes de partirmos para a análise de duas variáveis específicas, é importante saber que os gráficos do tipo scatterplot são muito úteis para analisar variáveis de quaisquer tipo:
sns.pairplot(data , vars=["price", "sqft_lot","sqft_living"])
plt.show()
Vamos separar as variáveis quantitativas e utilizar uma matriz de correlação de Pearson para checar quais as relações entre as mesmas:
cor=data[["price","sqft_living","sqft_lot"]].corr()
cor.index=['Preço', 'Área do imóvel', 'Área do lote']
cor.columns=['Preço', 'Área do imóvel', 'Área do lote']
cor
Assim como já fizemos, vamos nos utilizar do heatmap para enxergar essa matriz de uma maneira informativa:
sns.heatmap(cor, cmap="Greys")
plt.show()
Percebemos que não há uma relação muito clara entra as variáveis "price" e "sqft_lot". Por outro lado, olhando para a variável "sqft_living", parece que há uma relação positiva forte entre esta e o preço. É possível observar as mesmas informações com outros tipos de gráficos. O seguinte gráfico é o gráfico com a densidade conjunta entre as variáveis:
plot=sns.jointplot(x=data["sqft_living"], y=data["price"], kind='kde')
plot.ax_joint.set_xlabel('Área do Imóvel')
plot.ax_joint.set_ylabel('Preço')
plt.show()
A relação positiva entre as variáveis é evidente, até mesmo olhando para o coeficiente de correlação de Pearson com o valor de 0,7, que é bem alto. Ao contrário do gráfico do tipo scatter, olhando para a densidade conjunta podemos realmente ter uma ideia de onde está concentrados os pontos da nossa base de dados olhando para as partes mais escuras. Assim como já fizemos, vamos restringir os eixos para uma melhor visualização da parte com mais concentração:
plot=sns.jointplot(x=data["sqft_living"], y=data["price"], kind='kde', xlim=(500,4000), ylim=(0,1200000))
plot.ax_joint.set_xlabel('Área do Imóvel')
plot.ax_joint.set_ylabel('Preço')
plt.show()
Como já temos a correlação de pearson calculada para as duas variáveis, podemos calcular também o Tau de Kendall para as duas variáveis:
import scipy.stats as stats
tau,_=stats.kendalltau(data["price"], data["sqft_living"])
print("O Tau de Kendall para as duas variáveis é de", tau)
Distribuição condicional¶
Acabamos de ver o conceito de distribuição conjunta de duas variáveis. O conceito de distribuição conjunta dá origem ao conceito de distribuição condicional. Quando falamos em distribuição condicional, estamos interessados na distribuição de uma das variáveis impondo algumas condições sobre as outras. Para o caso discreto, temos que a distribuição de uma variável aleatória $X$ condicionada a outra variável $Y$ é dada por:
\begin{equation} P(X=x |Y=y)=\frac{P(X=x, Y=y)}{P(Y=y)} \end{equation}Como exemplo: primeiramente, jogamos uma moeda, sendo que cara vale 1 e coroa vale 0. Se tirarmos cara jogamos a moeda novamente, mas se tirarmos coroa, jogamos um dado honesto de 6 lados. As pontuações das duas jogadas são dadas por $X_1$ e $X_2$. Qual, por exemplo, a probabilidade de se pontuar 3 na segunda jogada, sendo que pontuamos 1 na primeira jogada? É zero! Pois é impossível pontuar 3 jogando uma moeda (tiramos cara na primeira jogada). Matematicamente fica assim:
\begin{equation} P(X_2=3 |X_1=1)=\frac{P(X_2=3 ,X_1=1)}{P(X_1=1)}=\frac{0}{1/2}=0 \end{equation}Um outro exemplo: qual a probabilidade de se pontuar 6 no total? A resposta fica assim:
\begin{equation} P(X_2+X_1=6)=P(X_2=6 ,X_1=0)=P(X_2=6 |X_1=0)P(X_1=0)=\frac{1}{6}\frac{1}{2}=\frac{1}{12} \end{equation}Quando lidamos com variáveis contínuas, trabalhamos com densidades condicionadas. Não vamos entrar em aspectos muito teóricos aqui, vamos trabalhar com um exemplo muito útil na prática.
OBS: mais detalhes teóricos em https://pt.wikipedia.org/wiki/Distribui%C3%A7%C3%A3o_de_probabilidade_condicional
As análises a seguir serão feitas com base nas distribuições condicionais dos preços dos imóveis. A distribuição desta variável será condicionada à variável "waterfront", que é igual a um se o imóvel fica de frente para o mar e 0 se o imóvel não fica de frente para o mar. Como o preço é uma variável continua, visualizaremos box-plots condicionais e densidades condicionais. Vamos começar pelas densidades:
groups = [0,1]
labels = ["Não","Sim"]
# Iterando
for group in groups:
subset = data[data['waterfront'] == group]
# Draw the density plot
sns.distplot(subset['price'], hist = False, kde = True,
kde_kws = {'linewidth': 3},
label = labels[group])
# Plot formatting
plt.legend(prop={'size': 10}, title = 'Em frente ao mar:')
plt.xlabel('Preço')
plt.ylabel('Densidade')
plt.show()
É possível ver que quando o imóvel está em frente ao mar, o preço segue uma tendência de alta. Vamos ver mais a fundo essas distribuições condicionais olhando para os box-plots:
sns.boxplot(x=data["waterfront"], y=data["price"])
plt.ylabel('Preço')
plt.xlabel('Em frente ao mar')
plt.show()
Agora veremos como uma distribuição conjunta pode ser condicionada a outra variável. Para isso, utilizaremos um scatter plot para visualizar as distribuições conjuntas do preço e e da área do imóvel condicionadas à variável "waterfront":
sns.lmplot(x="sqft_living", y="price", data=data, fit_reg=False, hue="waterfront", legend=False, height=5)
plt.legend(prop={'size': 10}, title = 'Em frente ao mar:')
plt.ylabel('Preço')
plt.xlabel('Área do imóvel')
plt.show()
Traçando uma reta de tendência:
sns.lmplot(x="sqft_living", y="price", data=data, fit_reg=True, hue="waterfront", legend=False, height=5)
plt.legend(prop={'size': 10}, title = 'Em frente ao mar:')
plt.ylabel('Preço')
plt.xlabel('Área do imóvel')
plt.show()
Exercício: que lição tiramos do gráfico acima?